Homework #11

All problems MUST be in a SINGLE *.m file and be in separate blocks using '%% Problem X'. Otherwise you will not receive credit. You may need additional files for class definitions or functions. See class webpage for naming convention.

Problem 1
Problem 2
Problem 3
Problem 4
Problem 5

Problem 1

Use a Markov-Chain and the Metropolis-Hastings algorithm to explore the the following 2D probability distribution:

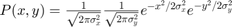
$P(x,y)=\frac{1}{\sqrt{2\pi\sigma_x^2}}\frac{1}{\sqrt{2\pi\sigma_y^2}}e^{-x^2/2\sigma_x^2}e^{-y^2/2\sigma_y^2}$

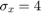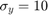where $\sigma_x=4$ and $\sigma_y=10$ .

Show a visual representation of the chain. Extra credit for particularly creative and clear visualization.

Problem 2

The file 'HW11Data.mat' contains two variables. 'T' indicates the measurement time. 'Volts' is the measured data. The theoretical model predicts that Voltage is proportional to time: 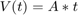$V(t)= A*t$ . Estimate 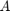$A$ from the data and find the standard error on 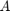$A$ using a Bayesian approach. The data has Gaussian type noise with 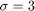$\sigma=3$ . Assume a uniform prior distribution on 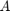$A$ . Hint: See March_30.m.

Problem 3

Make a GUI that plots the quantum mechanical probability distribution of a particle in a 1D box. Assume the particle is in an energy eigenstate. You should be able to select or type $n$ to plot a particular eigenstate.

Problem 4

Use the symbolic toolbox to find the analytical expressison for inverse of the matrix 'A' where

 
A =
 
[ a, b]
[ c, d]

Problem 5

Use the symbolic toolbox to find the integral of 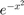$e^{-x^2}$ over all x.