Contents

Ising Model

The Ising model considers a lattice of paricles that have up or down spin. The total energy is given by the interaction of nearest neighbors and interaction of the spin with an external field.

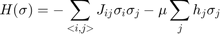
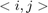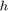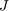Where the means adjacent particles, is the field, is the spin, which can be either -1 or 1, and is the interaction energy.

https://en.wikipedia.org/wiki/Ising_model

The 1D Ising Model

clc
close all
clear all

Beta=1;         %1/KbT
J=0;            %Interaction Strength
B=2;            %Magnetic Field
N=40;           %Number of spins

%Start with random orientation
Spins=double(randn(N,1)>0);
Spins(Spins==0)=-1;

%Plot Spins
X=(1:N)';
Y=Spins==-1;
FigH=figure;
FigH.Position=[200,300,900,400];
quiver(X,Y,X*0,Spins,0,'linewidth',2)
axis([0 N+1 -1 2])
s=sprintf('Beta=%g, J=%g, B=%g',Beta,J,B);
title(s)

%Setup so we stop when figure is closed
FigH.CloseRequestFcn='Go=0;';
Go=1;

%Run Markov Chain Monte Carlo
NChain=1000000;
nn=0;
while Go
    nn=nn+1;    %counter for display

    %Make test jump

    %Pick site and flip spin
    ID=ceil(N*rand);
    SpinsTest=Spins;
    SpinsTest(ID)=-Spins(ID);

    %Energy from nearest neighbor interactions
    E_Spin=J*(Spins(1:end-1).*Spins(2:end)+Spins(1)*Spins(end));
    E_SpinTest=J*(SpinsTest(1:end-1).*SpinsTest(2:end)+SpinsTest(1)*SpinsTest(end));

    %Energy from Interactions with feild
    E_Field=-B*sum(Spins);
    E_FieldTest=-B*sum(SpinsTest);

    %Total Energy (Hamiltonian)
    H=E_Spin+E_Field;
    HTest=E_SpinTest+E_FieldTest;

    %Test acceptance probability for Metropolis-Hastings
    Alpha=exp(-Beta*(HTest-H));

    %Metropolis-Hastings rule
    if rand()< (Alpha)
        Spins(ID)=-Spins(ID);
    end

    ShowIter=1;
    %Show every ShowIter interations
    if nn/ShowIter==round(nn/ShowIter)
        figure(FigH);
        hold off
        Y=Spins==-1;
        quiver(X,Y,X*0,Spins,0,'linewidth',2)
        axis([-1 N+1 -3 4])
        title(s)
        hold on
        quiver(0,0,0,B,0,'linewidth',2)
        legend('Spins','Field')
        pause(.1)
    end
end
delete(FigH)
figure;
hold off
Y=Spins==-1;
quiver(X,Y,X*0,Spins,0,'linewidth',2)
axis([-1 N+1 -3 4])
title(s)
hold on
quiver(0,0,0,B,0,'linewidth',2)
legend('Spins','Field')

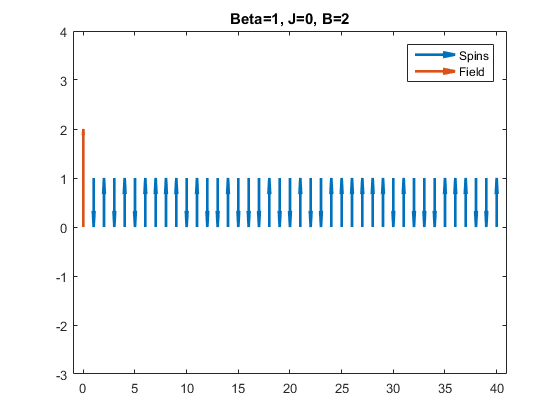
2D Ising Model

Same rules as the 1D Ising model. Neighbors are the 4 closest spins. In 2D there is phase transition at -1/(Beta*J)=2/log(1+sqrt(2))

clc
close all
clear all

Beta=10;         %1/KbT
J=-.2;            %Interaction Strength
B=0;            %Magnetic Field
N=100;           %Number of spins

2/log(1+sqrt(2))
-1/(Beta*J)

%Start with random orientation
Spins=double(randn(N,N)>0);
Spins(Spins==0)=-1;

%Plot Spins
FigH=figure;
%FigH.Position=[200,200,900,400];
imshow(Spins,[],'InitialMagnification',400)
s=sprintf('Beta=%g, J=%g, B=%g',Beta,J,B);
title(s)

%Setup so we stop when figure is closed
FigH.CloseRequestFcn='Go=0;delete(FigH)';
Go=1;

%Run Markov Chain Monte Carlo
NChain=1000000;
nn=0;
while Go
    nn=nn+1;    %counter for display

    %Make test jump

    %Pick site and flip spin
    IDX=ceil(N*rand);
    IDY=ceil(N*rand);
    SpinsTest=Spins;
    SpinsTest(IDX,IDY)=-Spins(IDX,IDY);

    %Energy from nearest neighbor interactions
    E_Spin=J*(sum(sum(Spins(1:end-1,:).*Spins(2:end,:)))+... %Y neighbor
        sum(Spins(1,:).*Spins(end,:))+... %Y periodic BC
        sum(sum(Spins(:,1:end-1).*Spins(:,2:end)))+... %X neighbor
        sum(Spins(:,1).*Spins(:,end))); %X periodic BC

    E_SpinTest=J*(sum(sum(SpinsTest(1:end-1,:).*SpinsTest(2:end,:)))+... %Y neighbor
        sum(SpinsTest(1,:).*SpinsTest(end,:))+... %Y periodic BC
        sum(sum(SpinsTest(:,1:end-1).*SpinsTest(:,2:end)))+... %X neighbor
        sum(SpinsTest(:,1).*SpinsTest(:,end))); %X periodic BC

    %Energy from Interactions with feild
    E_Field=-B*sum(Spins(:));
    E_FieldTest=-B*sum(SpinsTest(:));

    %Total Energy (Hamiltonian)
    H=E_Spin+E_Field;
    HTest=E_SpinTest+E_FieldTest;

    %Test acceptance probability for Metropolis-Hastings
    Alpha=exp(-Beta*(HTest-H));

    %Metropolis-Hastings rule
    if rand()< (Alpha)
        Spins(IDX,IDY)=-Spins(IDX,IDY);
    end

    ShowIter=1000;
    %Show every ShowIter interations
    if (nn/ShowIter==round(nn/ShowIter))
        pause(.01);if ~Go;break;end % Time to process closed figure
        figure(FigH);
        try
            imshow(Spins,[],'InitialMagnification',400)
        catch
        end
        pause(.01)
    end
end

ans =

    2.2692


ans =

    0.5000

Published with MATLAB® R2015b