Fraunhofer Diffraction and the 2D Fourier Transform; Solving the Heat/Diffusion Equation with Fourier Series

Contents

Fraunhofer Diffraction and the 2D Fourier Transform

Reference:

https://en.wikipedia.org/wiki/Fraunhofer_diffraction_%28mathematics%29

The complex amplitude of a diffracted wave far from an aperture can be calculated using the Fraunhofer diffraction integral:

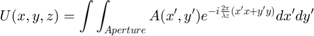
$$U(x,y,z)=\int\int_{Aperture} A(x',y') e^{-i \frac{2\pi}{\lambda z} (x'x+y'y)} dx'dy'$$

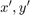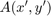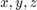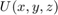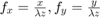$x',y'$ are the coordinates across the aperture, $A(x',y')$ is the complex amplitude across the aperture, and $x,y,z$ are the coordinates at the screen. The complex amplitude at each position $U(x,y,z)$ can be seen as the 2D Fourier coefficient calculated for the frequency $f_x=\frac{x}{\lambda z},f_y=\frac{y}{\lambda z}$.

The 2D Fourier transform

The two dimensional fourier transform is computed using 'fft2'. Let's try a simple example to demonstrate the 2D FT.

lambda=10;  %Try adjusting and look at the result.
k=2*pi/lambda;
[X,Y]=meshgrid(1:200,1:200);
kx=k*.2;
ky=k*.4;

Wave1=real(exp(i*k*X));
Wave2=real(exp(i*(kx*X+ky*Y)));
%Wave=ones(size(X));
Wave=Wave1+Wave2;
Noise=10*randn(size(Wave));
Wave=Wave+Noise;
figure;imshow(Wave,[]);title('Wave')

F_Wave=fft2(Wave);
figure;imshow(abs(F_Wave),[]);title('2D FFT of Wave')
F_Wave_Shift=fftshift(F_Wave);
figure;imshow(abs(F_Wave_Shift),[]);title('2D FFT of Wave, DC at Center.')

The Circular Aperture

Let's revisit diffraction from a circular aperture.

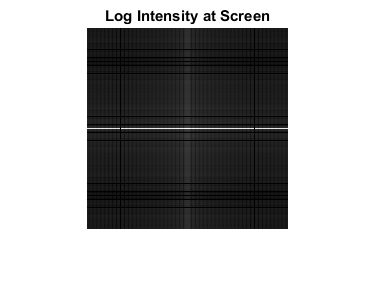
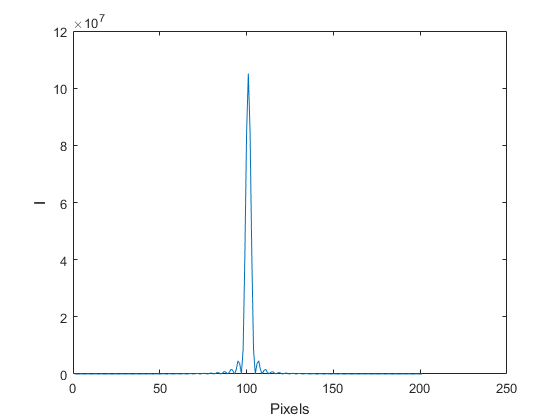
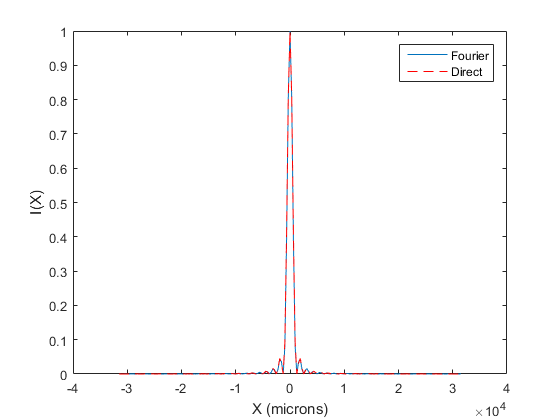
Lambda=.633;        %Wavelength of laser (micron)
D=50;               %Diameter of aperture (micron)
Z_Meters=.1;        %Screen distance in meters
Z=Z_Meters*10^6;    %Screen distance in microns

MeshSpacing=1;      %Sampling across aperture (micron)
MeshSize=200;       %Size of Screen (micron)

%Calculate and show the Amplitude across the aperture.
[XGrid,YGrid]=meshgrid((-MeshSize/2:MeshSpacing:MeshSize/2),(-MeshSize/2:MeshSpacing:MeshSize/2));
R=sqrt(XGrid.^2+YGrid.^2);
A=R<=D/2;  %The Amplitude across aperture (plane wave has constant amplitude, phase)
figure;imshow(A);title('Amplitude Across Aperture')

%Do the the 2D fft and show the result.
U=fftshift(fft2(A));
I=abs(U).^2;
figure;imshow(I,[]);title('Intensity at Screen')
figure;imshow(log(I),[]);title('Log Intensity at Screen')
figure;plot(I(101,:));xlabel('Pixels');ylabel('I')

% Now let's figure out the spacing of the pixels in I.
% The spacing of frequencies in the Fourier transform is 1/L
SZ=size(A,1);
FrequencySampling=1/(SZ*MeshSpacing); %units of 1/microns
[FGridX,FGridY]=meshgrid((0:SZ-1),(0:SZ-1));
FGridX_Shift=fftshift(FGridX);
FGridX_Shift(FGridX_Shift>SZ/2)=FGridX_Shift(FGridX_Shift>SZ/2)-SZ;
FGridY_Shift=fftshift(FGridY);
FGridY_Shift(FGridY_Shift>SZ/2)=FGridY_Shift(FGridY_Shift>SZ/2)-SZ;

FX=FGridX_Shift*FrequencySampling;
FY=FGridY_Shift*FrequencySampling;
X=FX*Lambda*Z;
Y=FY*Lambda*Z;

% Plot with units
I_norm=I/max(I(:));
X_center=X(101,:)+eps;
figure
plot(X_center,I_norm(101,:));xlabel('X (microns)');ylabel('I(X)')

% Compare to Airy disc
k=2*pi/Lambda;
a=D/2;
SinTheta=X_center./sqrt(X_center.^2+Z.^2);
I_Airy=(besselj(1,k*a*SinTheta)./(k*a*SinTheta)).^2;
I_Airy_norm=I_Airy/max(I_Airy(:));

hold on
plot(X_center,I_Airy_norm,'r--')
legend('Fourier','Direct')

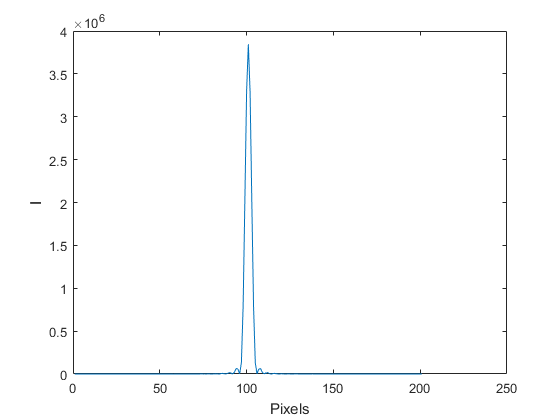
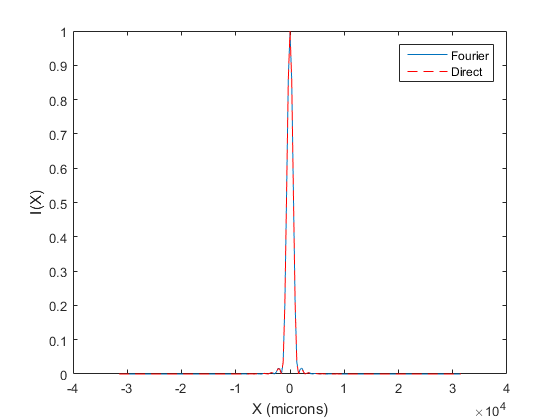
The Finite-Width Single Slit

lambda=.633;        %Wavelength of laser (micron)
a=50;               %Diameter of aperture (micron)
Z_Meters=.1;        %Screen distance in meters
Z=Z_Meters*10^6;    %Screen distance in microns

MeshSpacing=1;  %Sampling across aperture (micron)
MeshSize=200;
[XGrid,YGrid]=meshgrid((-MeshSize/2:MeshSpacing:MeshSize/2),(-MeshSize/2:MeshSpacing:MeshSize/2));
R=abs(XGrid);
A=R<=(a/2);  %The Amplitude across aperture
figure;imshow(A);title('Amplitude Across Aperture')

U=fftshift(fft2(A));
I=abs(U).^2;
figure;imshow(I,[]);title('Intensity at Screen')
figure;imshow(log(I),[]);title('Log Intensity at Screen')
figure;plot(I(101,:));xlabel('Pixels');ylabel('I')

% Now let's figure out the spacing of the pixels in I.
% The spacing of frequencies in the Fourier transform is 1/L
SZ=size(A,1);
FrequencySampling=1/(SZ*MeshSpacing); %units of 1/microns
[FGridX,FGridY]=meshgrid((0:SZ-1),(0:SZ-1));
FGridX_Shift=fftshift(FGridX);
FGridX_Shift(FGridX_Shift>SZ/2)=FGridX_Shift(FGridX_Shift>SZ/2)-SZ;
FGridY_Shift=fftshift(FGridY);
FGridY_Shift(FGridY_Shift>SZ/2)=FGridY_Shift(FGridY_Shift>SZ/2)-SZ;

FX=FGridX_Shift*FrequencySampling;
FY=FGridY_Shift*FrequencySampling;
X=FX*Lambda*Z;
Y=FY*Lambda*Z;

% Plot with units
I_norm=I/max(I(:));
X_center=X(101,:)+eps;
figure
plot(X_center,I_norm(101,:));xlabel('X (microns)');ylabel('I(X)')

% Compare to Theory
k=2*pi/Lambda;
SinTheta=X_center./sqrt(X_center.^2+Z.^2);

%Theory (See also Mar_23.m)
% The FT of the 'rect' function is the 'sinc' function.
%Make our own sinc function
mysinc=@(x)sin(pi*x)./(pi*x);
SinTheta=X_center./sqrt(Z.^2+X_center.^2);
SingleSlitDif=mysinc(SinTheta/Lambda*a).^2;

hold on
plot(X_center,SingleSlitDif,'r--')
legend('Fourier','Direct')


Published with MATLAB® R2015b