Homework #4

All problems must be in a single *.m file. You may need an additional files for a functions or class definitions. Make a separate block in the code for each problem. Do not submit individual files for each problem. See previous solutions.

Problem 1 (2 Points)
Problem 2 (1 Point)
Problem 3 (1 Point)
Problem 4 (1 Point)
Problem 5 (1 Point)

Problem 1 (2 Points)

The Maxwell-Boltzmann distribution describes the distribution of particle energies, velocities, or speeds in an ideal gas. The velocity distribution for each Cartesian dimension is a Gaussian distribution with

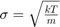$\sigma=\sqrt{\frac{kT}{m}}$ .

For 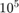$10^5$ particles, draw $x,y,z$ velocity components from this distribution. Use the result to calculate the speed and energy of each particle. Use histograms and overlayed plots to show that the speed and energy distribution of your particles match

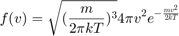
$f(v)=\sqrt{ (\frac{m}{2\pi kT})^3 } 4 \pi v^2 e^{-\frac{mv^2}{2kT}}$

and

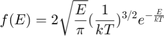
$f(E)=2\sqrt{\frac{E}{\pi}}(\frac{1}{kT})^{3/2}e^{-\frac{E}{kT}}$

respectively. Use Nitrogen at STP for your calculations. Plots should have units indicated.

Problem 2 (1 Point)

Use the Inversion method to generate random numbers from the standard (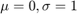 $\mu=0, \sigma=1$ ) Normal distribution using 'rand'. Convince the grader it is working using a histogram. Hint: 'help erf'

Problem 3 (1 Point)

A simple, and somewhat accuate method for generating random numbers from the standard normal distibution makes use of the Central Limit Theorem. Show

sum(rand(12,1))-6

produces numbers similar to randn(). Why does this work? What is the variance of a uniform distibution on 0 to 1? Hint: 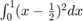$\int_0^1(x-\frac{1}{2})^2dx$

Problem 4 (1 Point)

On average, a particular constant-rate process generates 4 events. What percentage of the time does it produce exactly 4 events?

Problem 5 (1 Point)