Homework #5
All problems must be in a single *.m file. You may need an additional files for a functions or class definitions. Make a separate block in the code for each problem. Do not submit individual files for each problem. See previous solutions.
Contents
Problem 1 (2 Points)
Use the symbolic toolkit to find the general solution of a damped harmonic ocsillator.
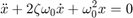
where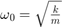 
.
Take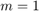 
and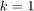 
and plot the result for an underdamped system where the mass is stretched away from equilibrium, held steady, then released.
Problem 2 (3 Points)
Create a 'RK4' class that uses the fourth-order Runge-Kutta method to numerically integrate an arbitrary ODE. Class properties should include a function handle (that will be used to calculate the rates of change of a vector parameter), the step size, and limits of integration. The methods should include a function for the calculation and a function for plotting.
Demonstrate the use of your class by numerically integrating the damped ocillator in Problem 1.
Demonstrate the use of the class to simulate the motion of a planet with a closed orbit.
Problem 3 (1 Point)
Create a movie of the under-damped ocsillator that shows the instantaneous position, along with the instantaneous velocity and force vectors.