Homework #8
All problems must be in a single *.m file. You may need additional files for functions or class definitions. Make a separate block in the code for each problem. Do not submit individual files for each problem. See previous solutions.
Contents
Problem 1 (3 Points)
Consider an electron that at t=0 has a Gaussian probability density in x, with size of a Hydrogen atom. Show an animation of the particle as its wave packet spreads to 10 times the original size. How long does it take? Estimate how long it would take to spread to 1 m. 1 Point of this problem is for the creation and use of a class.
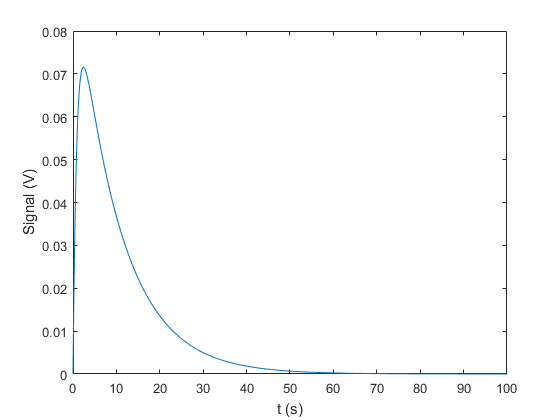
Problem 2 (1 Point)
Photomultiplier Tubes (PMTs) produce a burst of current in response to light incident on the photocathode and this can be seen as a voltage pulse on an oscilloscope. For a particular PMT, a single photo-electron gernerates the response given below. Use ffts to convolve the instrument response with a signal generated from a constant rate process.
Problem 3 (1 Point)
Use Fourier transforms to calculate the far-field diffraction pattern created by laser light incident on a finte-width double slit. Compare your result to theory.
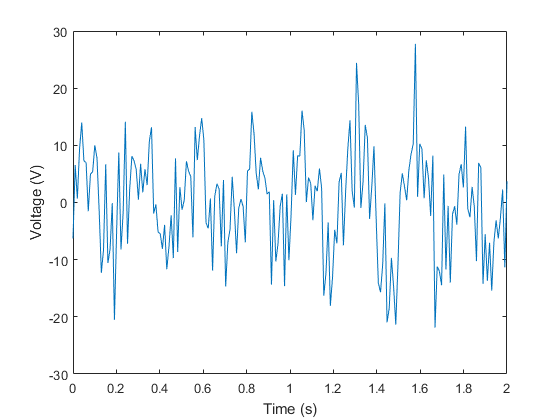
Problem 4 (1 Point)
Find the amplitude and frequency of the wave that is buried in the noisy data set 'HW8_NoisyData.mat' and plotted below.